Sistemi a stati finiti

(la videolezione) Nella quotidianità siamo letteralmente circondati da automi: sono infatti automi (anche detti sistemi a stati finiti) la lavatrice, la lavastoviglie, il frullino, gli orologi che si vincono nei detersivi, i sistemi di controllo di apertura/chiusura delle banche, i bancomat, i sistemi di controllo degli ascensori, i distributori automatici di bevande, i distributori di gettoni telefonici, i distributori automatici di benzina. Ma sono rappresentabili come automi anche "cose" più astratte come automi riconoscitori di sequenze, automi analizzatori di linguaggio, automi traduttori, automi decodificatori. I computer sono anch'essi automi, in particolare automi a programma, cioè possono svolgere il ruolo di un automa o di un altro a seconda del programma che in quel momento sta "girando".  In realtà il sistema a stati finiti (o macchina a stati finiti) è un modello matematico fondamentale per descrivere comportamenti di sistemi logici, informatici e automatici.

Prima di addentrarci nel sistema, occorre capire l'unità fondamentale che lo compone: lo stato. Uno stato è una condizione ben definita in cui un sistema può trovarsi in un dato momento. Il telefono, quando riceve una chiamata, può essere in uno di questi stati: IN ATTESA, SQUILLARE, IN CONVERSAZIONE. Uno stato cattura una "fotografia" della situazione del sistema, ignorando tutto il resto.

Un Sistema a Stati Finiti è, quindi, un modello matematico composto da un numero finito di stati. Il sistema può essere in uno e un solo stato alla volta. La magia avviene quando qualcosa lo spinge a passare da uno stato all'altro: questa "spinta" è chiamata transizione.

Come si fa a rappresentare visivamente questo insieme di stati e transizioni? Si utilizza uno strumento elegante e intuitivo: il Grafo di Transizione.

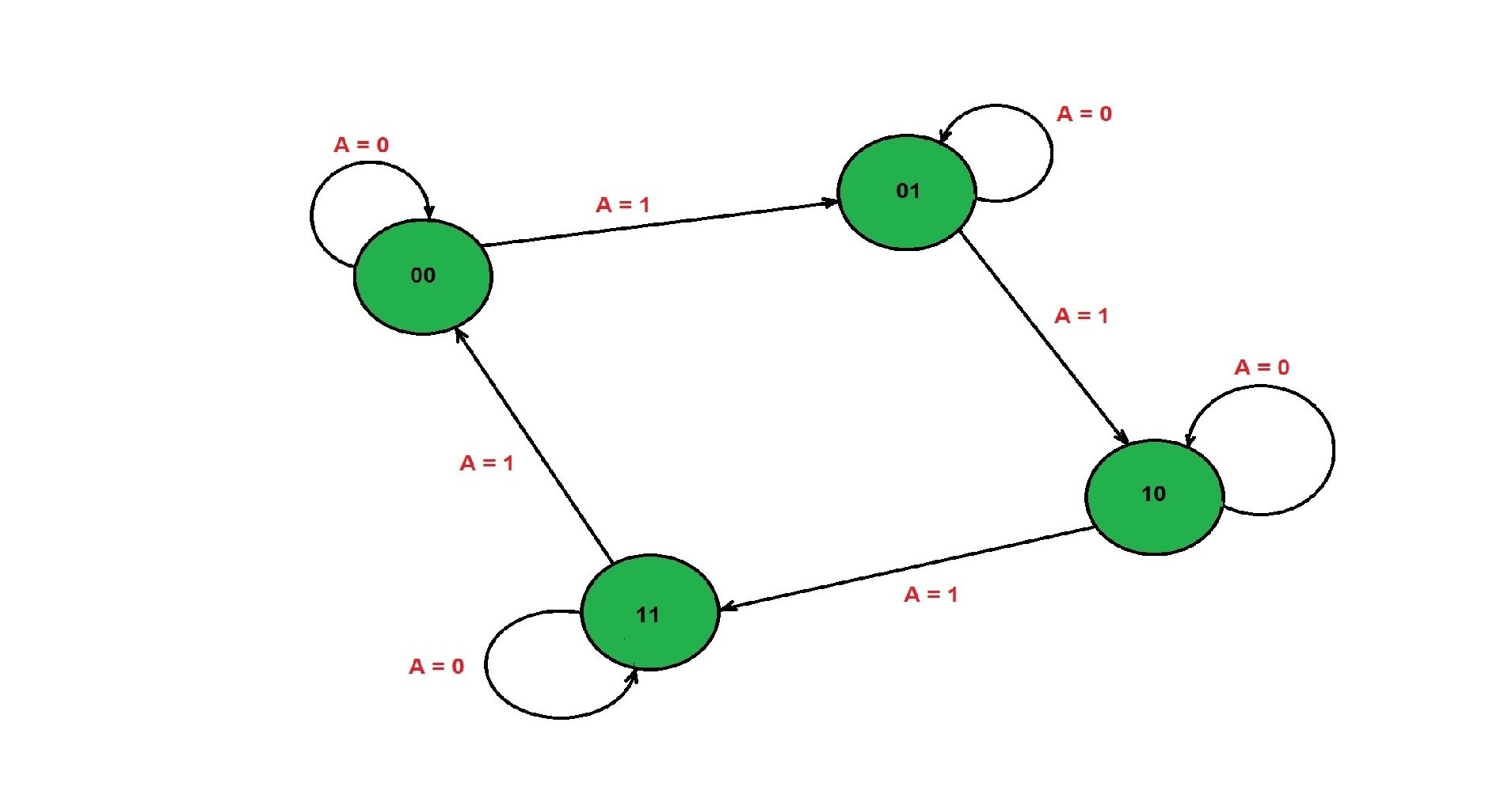
Immaginiamo, ad esempio, una mappa metropolitana:

I Nodi (cerchi) sono le stazioni: rappresentano i possibili stati del sistema.

Gli Archi (frecce) sono i binari: rappresentano le transizioni da uno stato all'altro. Su ogni freccia c'è un'etichetta che indica l'evento che causa quella transizione.

Facciamo l'esempio di una serratura a combinazione. Immaginiamo che la combinazione che provoca l'apertura sia "1-2-3".

Stati:

BLOCCATA: lo stato iniziale, la porta è chiusa.

CIFRA_1: l'utente ha digitato correttamente la prima cifra (1).

CIFRA_2: l'utente ha digitato correttamente le prime due cifre (1,2).

SBLOCCATA: la porta si apre!

Eventi: La pressione dei tasti 1, 2, 3 e RESET.

Ecco come potrebbe essere il grafo di transizione:

Da [BLOCCATA]:

Se si preme 1 -> si va a [CIFRA_1].

Se si preme qualsiasi altro tasto -> si rimane in [BLOCCATA].

Da [CIFRA_1]:

Se si preme 2 -> si va a [CIFRA_2].

Se si preme RESET oppure 3 -> si torna a [BLOCCATA].

Se si preme il tasto 1 -> si rimane in [CIFRA_1] .

Da [CIFRA_2]:

Se si preme 3 -> si va a [SBLOCCATA].

Se si preme RESET oppure 2  -> si torna a [BLOCCATA].

Se si preme un tasto 1 -> si torna a [CIFRA_1] .

Questo modello ci permette di tracciare ogni possibile percorso che l'utente può compiere, gestendo sia i successi che gli errori.

I sistemi a stati finiti e i loro grafi sono onnipresenti, anche se spesso non si vedono:

Informatica e Programmazione: Sono il cuore di molti algoritmi, compilatori (per l'analisi del codice), e protocolli di rete. Sviluppatori e ingegneri li usano per modellare il comportamento di un software in modo chiaro e privo di ambiguità, prima di scrivere una sola riga di codice.

Elettronica e Automazione: Controllano i semafori, i distributori automatici, i sistemi di allarme e i circuiti digitali.

Game Development: Sono fondamentali per gestire il comportamento dei personaggi (NPC). Un nemico in un videogioco può avere stati come  PATAGLIAMENTO, ALLERTA, ATTACCO, FUGA, e le transizioni sono determinate dalle azioni del giocatore.

Design dell'Interfaccia Utente (UI/UX): Modellano il flusso di un'app o di un sito web. Cosa succede quando un utente clicca "Avanti", "Indietro" o "Salva"? Ogni schermata e ogni azione può essere rappresentata come uno stato e una transizione.

I sistemi a stati finiti, però, diventano rapidamente ingestibili e incredibilmente complessi quando si deve modellare un sistema con una memoria interna elaborata o un numero enorme di condizioni. Immaginiamo di voler modellare il comportamento di un intero ufficio postale: il numero di stati possibili (ogni cliente in una fase diversa) esploderebbe.

In termini più rigorosi, è possibile sintetizzare definendo un sistema a stati finiti (automa) come un modello costituito da:

Un insieme finito di stati

Un insieme di input (o eventi)

Una funzione di transizione che dice come il sistema passa da uno stato all’altro in base all’input

Uno stato iniziale e, in certi casi, uno o più stati finali.

Lo schema a blocchi in basso descrive l'architettura di un generico sistema a stati finiti. I blocchi contrassegnati con la M rappresentano elementi di memoria (solitamente flip-flop tipo D).